Con questo secondo articolo dedicato al nostro satellite naturale non voglio semplicemente chiudere un argomento, piuttosto aprire un nuovo capitolo di approfondimento suscettibile di sviluppi futuri. Dopo la sessione osservativa del 1 agosto dove avevo ripreso alcune foto della superficie lunare a basso ingrandimento, il giorno 7 e 11 agosto ho tentato un’indagine più approfondita con foto ad una risoluzione maggiore utilizzando sia una lente di Barlow 2x che di fatto raddoppia la lunghezza focale del telescopio, sia un oculare ortoscopico da 9 millimetri per sfruttare il metodo della “proiezione dell’oculare” sulla camera CCD utilizzata per le riprese.
Tecniche di ripresa
Ritengo sia d’obbligo a questo punto chiarire qualcosa sulle tecniche di ripresa, non tanto per gli astrofili più navigati ma per quelli che si stanno avvicinando per la prima volta all’affascinante mondo dell’astrofotografia e delle riprese planetarie e lunari in particolare. Esistono quattro metodi diversi per riprendere fotografie attraverso un telescopio:
- Fuoco diretto
- Interposizione lente di Barlow
- Proiezione dell’oculare
- Metodo Afocale
Il primo metodo consiste nel porre la macchina fotografica senza obiettivo o la camera CCD al posto dell’oculare, in questo modo si ottiene la massima luminosità possibile dla sistema ma anche il minimo ingrandimento. Il metodo 2 prevede l’interposizione di un particolare sistema ottico, costituito da due o tre lenti, tra il telescopio e il sistema di ripresa, senza il prorpio obiettivo nel caso di fotocamera: il sistema ottico è chiamato “lente di Barlow” e provvede ad aumentare la lunghezza focale equivalente dell’intero insieme grazie al suo sitema di lenti negative. Normalmente una lente di Barlow raddoppia la lunghezza focale di un telescopio (Barlow 2x) ma esistono Barlow che triplicano (3X) o addirittura quintuplicano (5x); chiaramente più una Barlow è “spinta” più aumentano i difetti ottici nell’immagine finale, quindi si può dire che il massimo utlizzabile per una Barlow normale è la 3x anche se sarebbe meglio limitarsi alla 2x e possibilmente scegliere le Barlow apocromatiche, costituite da tre o più lenti, a differenza delle normali acromatiche con solo due lenti. In sostanza una lente di Barlow è l’equivalente astrofotografico di un duplicatore di focale fotografico, solo che quest’ultimo è normalmente costituito da cinque o sei lenti: in astronomia la quantità di luce che ci arriva dagli astri è quasi sempre molto poca, per cui si tende a limitare il più possibile il numero di lenti in un sistema ottico proprio per evitare eccessive dispersioni e perdite di luminosità. Con il terzo metodo si entra appieno nel mondo della fotografia planetaria e lunare ad alta risoluzione in quanto il sistema permette di ottenere forti ingrandimenti, anche superiori a quelli ottenibili con le lenti di Barlow.
 Schema ottico completo del metodo di proiezione dell’oculare con una camera CCD utilizzata per la ripresa (dal sito astronomysource)
Schema ottico completo del metodo di proiezione dell’oculare con una camera CCD utilizzata per la ripresa (dal sito astronomysource)
 Come si realizza in pratica il metodo della proiezione dell’oculare, in questo caso viene utilizzato un anello adattatore (T-Ring) a cui sarà poi applicata una fotocamera reflex senza obiettivo (dal sito astronomysource)
Come si realizza in pratica il metodo della proiezione dell’oculare, in questo caso viene utilizzato un anello adattatore (T-Ring) a cui sarà poi applicata una fotocamera reflex senza obiettivo (dal sito astronomysource)
Le due immagini precedenti illustrano in maniera piuttosto evidente come funziona e come si mette in pratica questo metodo. Infine il quarto metodo prevede di utilizzare il sistema ottico completo del telescopio (obiettivo + oculare) con quello completo di una fotocamera, compreso il suo obiettivo: in pratica chiunque fotografi utilizzando uno smartphone appoggiato sull’oculare del telescopio utilizza il metodo Afocale. Tra tutti quelli descritti quello Afocale è senz’altro il peggiore in termini sia di qualità dell’immagine finale sia di stabilità meccanica dell’intero sistema; può essere considerato un punto di inizio ma se si vuole ottenere qualcosa di meglio bisogna necessariamente evolversi verso gli altri metodi, attrezzandosi di conseguenza.
La Teoria
Qualche formula e un paio di calcoli non credo facciano male, anzi ritengo siano a questo punto quanto mai opportuni per inquadrare meglio le metodologie; ci limiteremo ad esaminare nel dettaglio i metodi 2 e 3, in quanto più inerenti all’argomento specifico della fotografia planetaria e lunare. La prima cosa che bisogna tenere presente è che, in campo astronomico, uno degli elementi più importanti in assoluto è il diametro del telescopio e questo per due motivi: uno perchè più luce si raccoglie meglio è e secondo perchè più grande è il diametro più aumenta il potere risolutivo, ovvero la capacità di riuscire a vedere separati due punti vicini. La formula empirica per calcolare il potere risolutivo di un telescopio è:
Pr = 120 / D
dove D è il diametro in millimetri della lente o dello specchio principale del telescopio, quella che raccoglie la luce dagli astri. Il potere risolutivo risultante è una misura angolare ed è espresso in secondi d’arco, ovvero in tremilaseicentesimi di grado e viene abbreviato dal simbolo “; quindi un telescopio con un diametro di 200 millimetri avrà un potere risolutivo di 0,6”, ovvero potrà risolvere oggetti con una separazione minima di 0,00017 gradi. Si tratta ovviamente di un valore teorico e il potere risolutivo reale dipenderà anche da altri fattori, come le condizioni del telescopio e, soprattutto, lo stato di turbolenza dell’atmosfera, quello che viene definito “seening”; quest’ultimo influenza pesantemente il potere risolutivo tanto che il valore teorico sarà raggiungibile solo in rarissime occasioni e la maggior parte delle volte bisognerà usare quello determinanto dal seening, anch’esso espresso in secondi d’arco. Il secondo elemento che bisogna esaminare è la lunghezza focale del telescopio: maggiore è la lunghezza focale e meno luminoso sarà lo strumento, come viene detto nel gergo astronomico. Una lunghezza focale corta, tipicamente 5 o 6 volte il diametro dell’obiettivo, è particolarmente adatta per un telescopio che dovrà mostrare preferibilmente oggetti deboli e diffusi, dove si potranno fotografare questi oggetti con tempi di esposizione abbastanza brevi ma non si potranno avere forti ingrandimenti. In effetti la formula per calcolare gli ingrandimenti risultanti è la seguente:
I = F / Fo
dove F è la lunghezza focale del telescopio e Fo la lunghezza focale dell’oculare utilizzato. Quindi si può vedere che a parità di oculare utilizzato un telescopio con una lunghezza focale 5 volte il diametro (definito come “rapporto d’apertura” ed indicato come f/5) potrà ingrandire molto meno di un telescopio che ha una lunghezza focale 10 volte il suo diametro (f/10): questo fattore è estremamente importante nell’osservazione visuale e fotografica dei pianeti. In effetti un’efficace combinazione di potere risolutivo ed ingrandimento permette di sfruttare al massimo un telescopio nelle osservazioni planetarie e lunari: un telescopio da 200 millimetri di diametro e 2000 millimetri di lunghezza focale (f/10), come lo Schmidt-Cassegrain che uso normalmente, ha un potere risolutivo teorico di 0,6″ ed equipaggiato con un oculare da 9 millimetri di focale potrà ingrandire visualmente 222 volte circa. Ma questo ingrandimento è quello ideale per poter osservare i più piccoli dettagli osservabili della Luna o di un pianeta? Purtroppo questa valutazione dipende fortemente dalle condizioni osservative del momento e non si possono dare riferimenti o formule valide in senso assoluto: si può però definire sia un ingrandimento minimo risolvente sia uno massimo, oltre il quale non sarebbe consigliabile andare per non degradare eccessivamente l’immagine. L’ingrandimento minimo risolvente si ottiene comparando il potere risolutivo dell’occhio umano con quello del telescopio, secondo la formula:
Imin = Pr(eye) / Pr (tele)
considerando che, in media, il potere risolutivo dell’occhio umano è di 100″, con il mio telescopio da 200 millimetri si ottiene un ingrandimento minimo risolvente pari a 167x. Questo numero indica quindi che tutti i dettagli che il mio occhio potrà percepire saranno già visibili a 167 ingrandimenti, supponendo di osservare in una serata con l’atmosfera molto stabile che permetta di raggiungere il potere risolutivo teorico del telescopio. Per contro l’ingrandimento massimo consigliabile può essere definito dalla formula empirica (Paolo Andrenelli, l’Astronomo Dilettante, Sansoni, 1968-1979):
Imax = 13,8 * RADQ(D)
dove RADQ è la radice quadrata e D il diametro in millimetri del telescopio. Quindi ancora per il mio Schmidt-Cassegrain troviamo un ingrandimento massimo di 195x. Questo non vuol dire che non si possa ingrandire di più, magari sfruttando anche una lente di Barlow; vuol dire semplicemente che a questi fattori d’ingrandimento si hanno già visibili tutti i dettagli possibili, almeno visualmente, e che ingrandire di più potrà solo evidenziarli meglio a patto che le condizioni di turbolenza atmosferica lo permettano. In alcune letterature si trova che l’ingrandimento massimo utilizzabile è addirittura pari a due volte il diametro del telescopio in millimetri, quindi arriviamo a 400x nel mio caso; ma ripeto che si tratta sempre di misure empiriche che devono dare più un orientamento piuttosto che una regola.
Dal punto di vista fotografico, invece, le regole sono un poco più precise e permettono di definire meglio tecniche e modalità di ripresa. Per “fotografiche” intendo ovviamente riprese con sistemi elettronici, in quanto il tempo delle emulsioni fotografiche è tramontato già da un bel pò; in questo senso farò riferimento indifferentemente sia a camere planetarie sia a fotocamere in quanto il meccanismo di acquisizione è assolutamente identico, ovvero sensori CCD. Fondamentale in campo fotografico è il concetto di “campionatura” ovvero la riproduzione più fedele possibile di un segnale continuo, come quello dell’immagine da un telescopio, da parte di un sensore CCD che per sua natura è discontinuo. Il criterio di campionamento (teorema del campionamento) enunciato dai matematici Harry Nyquist e Claude Shannon prevede che sia possibile registrare in maniera adeguata un segnale analogico in formato digitale, a patto che venga effettuato un adeguato numero di campionamenti: questi non devono essere più grandi della metà del più piccolo dettaglio visibile. Nel caso della registrazione da parte di CCD di immagini astronomiche, il più piccolo dettaglio visibile che il telescopio è in grado di mostrare deve essere registrato da almeno due pixel. Per fare un esempio concreto, utilizzando la mia camera CCD ZWO ASI 120MC dotata di un sensore delle dimensioni di 4,8 x 3,6 millimetri con una risoluzione massima di 1280×960 pixels, ogni pixel ha le dimensioni di 3,75 micron, ovvero 0,00375 millimetri; il criterio di campionamento stabilisce che per poter sfruttare al meglio il potere risolutivo del mio telescopio Schmidt-Cassegrain da 200 millimetri di diametro e 2000 millimetri di lunghezza focale, la scala d’immagine dovrà essere di 0,3″ per pixel, essendo il potere risolutivo teorico del telescopio pari a 0,6″. La formula per determinare la scala d’immagine del telescopio con il sensore utilizzato è:
S = d * 206,28 / F
dove S è la scala d’immagine secondi d’arco per pixel, d le dimensioni di un singolo pixel in micron e F la focale del telescopio. Il risultato nel mio caso è quindi pari a circa 0,39″/pixel, un poco superiore a quello auspicabile di 0,3″; a questo è facile calcolare la lunghezza focale necessaria affinchè si realizzino le condizioni minime di scala d’immagine, grazie alla formula:
F = d * D * 3,438
dove D è il diametro del telescopio in millimetri. Sempre nel mio caso risulta una lunghezza focale ottimale per la campionatura pari a circa 2578 millimetri. Ecco quindi che risulta necessario aumentare la lunghezza focale originale del telescopio fino a portarla almeno al valore ottimale, oppure anche un valore superiore a patto che le condizioni atmosferiche (seening) della serata lo permettano. In realtà talvolta è possibile spingere la lunghezza focale oltre il limite indicato dalla campionatura ottimale o come si dice in gergo sovracampionare, anzi qualche volta è quasi necessario in quanto nelle formule sopra riportate non vengono considerati alcuni effetti come la tipologia di costruzione della matrice CCD che prevede degli spazi vuoti tra un pixel ed un altro adiacente; in questi spazi vuoti possono perdersi parti d’informazione del segnale analogico che non vengono campionate e quindi sovracampionando si prendono in considerazione più pixel per la campionatura. Inoltre con tempi di esposizione brevissimi come quelli richiesti dalle foto planetarie e lunari è possibile minimizzare gli effetti della turbolenza atmosferica: la realizzazione di file video (formato AVI non compresso) permette di avere a disposizione una grande quantità di frame con tempi di esposizione dell’ordine di decimi di secondo ognuno ed è qundi anche possibile utilizzare tecniche di ricostruzione dell’immagine sotto forma di complessi algoritmi di deconvoluzione che possono portare fino al raddoppio del potere risolutivo reale. Con questi ulteriori elementi di valutazione è quindi assolutamente lecito prevedere l’utilizzo non solo della lente di Barlow (metodo 2 della lista iniziale) per aumentare la focale del telescopio ma anche oculari per il metodo della proiezione (numero 3). Nel caso della lente di Barlow i calcoli sono abbastanza semplici: la lunghezza focale del telescopio viene praticamente raddoppiata e il nuovo valore entra a far parte dei calcoli. Con il metodo della proiezione dell’oculare le cose sono invece leggermente diverse, in quanto la focale complessiva del sistema deve essere calcolata attraverso una formula:
Feq = F * ((T / Fo) – 1)
dove Feq è la focale equivalente del sistema ottico, cioè la nuova focale del telescopio vista dal punto di fuoco sul sensore CCD, Fo è ancora la focale dell’oculare, F quella dell’obiettivo del telescopio e T il “tiraggio” ovvero la distanza dall’ultima lente dell’oculare al sensore CCD dove si forma l’immagine. Come esempio vediamo ancora il caso delmio telescopio, utilizzando un oculare ortoscopico da 9 millimetri ed un tiraggio misurato pari a 30 millimetri: in queste condizioni la focale equivalente risultante è pari a 4667 millimetri, quindi leggermente superiore a quello ottenibile con la Barlow 2x ed in piena sovracampionatura.
Immagini
A questo punto, con il piccolo bagaglio teorico che abbiamo acquisito, vediamo qualche immagine e cerchiamo di analizzarla. In questa sede vedremo alcune immagini della Luna riprese, come accennato nell’introduzione, nelle giornate del 7 e 11 agosto 2020 con il nostro satellite in fase calante e ben visibile dopo la mezzanotte locale. L’intero set di immagini ripreso nelle due serate include anche una ricerca dettagliata riguardante alcune particolari formazioni lunari chiamati “Domi“, da latino Domus, ovvero “case”. Con questa terminologia vengono definite delle strutture a forma di cupola, somiglianti a dei vulcani a scudo come quelli delle Hawaii ma molto più bassi (al massimo poche centinaia di metri in altezza) e che possono raggiungere un’estensione di qualche decina di chilometri. Si tratta probabilmente dei veri ed unici vulcani lunari, in quanto tutti gli altri crateri sono chiaramente di origine meteorica; possono avere un piccolo cratere sulla loro sommità, hanno una bassissima pendenza ed il magma che è fuoriuscito dal loro interno e che ha contribuito alla loro formazione è dello stesso tipo di quello presente nei Mari lunari. Si trovano principalmente sui bordi delle vaste distese laviche ed in vicinanza di fratture o faglie nella superficie. Nella seconda parte di questo articolo affronterò una trattazione più estesa e dettagliata dei Domi lunari, corredando il tutto con alcune immagini riprese ad alta risoluzione; qui invece vediamo altre immagini riprese sia basso ingrandimento (fuoco diretto del telescopio), sia con la lente di Barlow e con la proiezione di un oculare ortoscopico da 9 millimetri ma nessuna di queste riporta dei Domi evidenti.
 In questa prima immagine ripresa a bassa risoluzione ho inquadrato la regione nord-orientale della superficie lunare con in evidenza il cratere Aristoteles. La lunghezza focale del telescopio Schmidt-Cassegrain da 200 mm di diametro era qui al suo valore normale, ovvero 2000 mm, in base alla formula:
In questa prima immagine ripresa a bassa risoluzione ho inquadrato la regione nord-orientale della superficie lunare con in evidenza il cratere Aristoteles. La lunghezza focale del telescopio Schmidt-Cassegrain da 200 mm di diametro era qui al suo valore normale, ovvero 2000 mm, in base alla formula:
w = 206265 * (2 * d) / F
si ottengono le dimensioni angolari in secondi d’arco del più piccolo particolare visibile, in questo caso otteniamo con d = 3,75 micron (0,00375 millimetri) avendo utilizzato la camera ZWO ASI 120MC un valore w di 0,77″; leggermente superiore al potere risolutivo massimo del telescopio. A questo punto è facile determinare le dimensioni reali di tale caratteristica, visto che la Luna in quella serata si trovava a circa 400.700 km di distanza dalla Terra (Delta) si applica la formula con w trasformato in gradi:
v = Delta * TAN(w)
si trova un valore di v pari a 1,5 km. In realtà questo valore si riferisce al più piccolo dettaglio visibile considerando questo come registrabile da due pixel adiacenti: in realtà per le condizioni viste nel paragrafo precedente tale valore appare abbastanza ottimistico, molto più realistico potrebbe essere considerare come il più piccolo dettaglio visibile quello registrabile da almeno una matrice di quattro pixel, questo porta il valore di v ad almeno 3 km.
 Questa seconda immagine è stata ripresa con l’ausilio della lente di Barlow 2x, raddoppiando quindi la focale del telescopio che raggiunge i 4000 mm equivalenti. La regione è sempre quella del cratere Aristoteles, il cratere più grande in alto. Utilizzando le stesse formule viste precedentemente ed applicando le medesime considerazioni sul numero di pixel necessari per registrare il dettaglio più piccolo visibile, si ottiene un valore di 1,5 km.
Questa seconda immagine è stata ripresa con l’ausilio della lente di Barlow 2x, raddoppiando quindi la focale del telescopio che raggiunge i 4000 mm equivalenti. La regione è sempre quella del cratere Aristoteles, il cratere più grande in alto. Utilizzando le stesse formule viste precedentemente ed applicando le medesime considerazioni sul numero di pixel necessari per registrare il dettaglio più piccolo visibile, si ottiene un valore di 1,5 km.
 Terza immagine ottenuta con il metodo della proiezione dell’oculare (9 mm ortoscopico) e centrata esattamente sul cratere Aristoteles. Si può notare che l’immagine non appare più nitida e definita come in quella a basso ingrandimento ed appare leggermente più degradata anche rispetto a quella ottenuta con la lente di Barlow 2x; tuttavia sono ancora ben visibili moltissimi dettagli superficiali con un buon grado di nitidezza. In questo caso la serata era particolamente favorevole ed il seening piuttosto buono. Considerando una focale equivalente di 4667 mm, in quanto ho utilizzato l’oculare da 9 mm, risulta che il dettaglio più piccolo visibile doveva essere di dimensioni angolari intorno ai 0,66″ quindi ancora al di sopra del massimo teorico possibile per il mio telescopio: il valore in km corrispondente è di circa 1,29. Si tenga presente che qualora le dimensioni angolari del dettaglio più piccolo visibile dovessero essere inferiori al potere risolutivo massimo teorico del telescopio, si dovrebbe usare esclusivamente quest’ultimo valore. Come termine di confronto si consideri che il cratere Aristoteles ha un diametro di circa 88 km
Terza immagine ottenuta con il metodo della proiezione dell’oculare (9 mm ortoscopico) e centrata esattamente sul cratere Aristoteles. Si può notare che l’immagine non appare più nitida e definita come in quella a basso ingrandimento ed appare leggermente più degradata anche rispetto a quella ottenuta con la lente di Barlow 2x; tuttavia sono ancora ben visibili moltissimi dettagli superficiali con un buon grado di nitidezza. In questo caso la serata era particolamente favorevole ed il seening piuttosto buono. Considerando una focale equivalente di 4667 mm, in quanto ho utilizzato l’oculare da 9 mm, risulta che il dettaglio più piccolo visibile doveva essere di dimensioni angolari intorno ai 0,66″ quindi ancora al di sopra del massimo teorico possibile per il mio telescopio: il valore in km corrispondente è di circa 1,29. Si tenga presente che qualora le dimensioni angolari del dettaglio più piccolo visibile dovessero essere inferiori al potere risolutivo massimo teorico del telescopio, si dovrebbe usare esclusivamente quest’ultimo valore. Come termine di confronto si consideri che il cratere Aristoteles ha un diametro di circa 88 km
 Riprendendo la prima immagine si può osservare nella sua parte più orientale il cratere Burg: in questa foto ripresa con la lente di Barlow 2x si può vedere il dettaglio di questo cratere, assolutamente circolare e del diametro di 40 km, e la regione immediatamente circostante. La distesa lavica che circonda il cratere è chiamata Lacus Mortis; poco distante il più grande cratere Hercules con un diametro di 70 km e con le pareti che si elevano fino a 3200 metri al di sopra del fondo del cratere stesso. Ricordo che i crateri appaiono ellittici per via della prospettiva con cui li vediamo dalla Terra. I dettagli più fini sono ancora ben visibili in questa immagine che ha una risoluzione massima di circa 1,5 km.
Riprendendo la prima immagine si può osservare nella sua parte più orientale il cratere Burg: in questa foto ripresa con la lente di Barlow 2x si può vedere il dettaglio di questo cratere, assolutamente circolare e del diametro di 40 km, e la regione immediatamente circostante. La distesa lavica che circonda il cratere è chiamata Lacus Mortis; poco distante il più grande cratere Hercules con un diametro di 70 km e con le pareti che si elevano fino a 3200 metri al di sopra del fondo del cratere stesso. Ricordo che i crateri appaiono ellittici per via della prospettiva con cui li vediamo dalla Terra. I dettagli più fini sono ancora ben visibili in questa immagine che ha una risoluzione massima di circa 1,5 km.
 Utilizzando ancora una volta il metodo della proiezione con l’oculare da 9 mm portiamo la risoluzione massima intorno ai 1,3 km ma l’immagine in questo caso perde notevolmente in qualità, anche con evidenti segni di aberrazione cromatica dovuta all’oculare e dagli effetti rifrangenti dell’atmosfera. In effetti il seening può facilmente variare durante la stessa serata in maniera imprevedibile. Malgrado tutto sono però riconoscibili una grande quantità di dettagli come piccoli crateri, creste, formazioni montuose e corrugamenti della superficie lavica proprio a ridosso del cratere Burg.
Utilizzando ancora una volta il metodo della proiezione con l’oculare da 9 mm portiamo la risoluzione massima intorno ai 1,3 km ma l’immagine in questo caso perde notevolmente in qualità, anche con evidenti segni di aberrazione cromatica dovuta all’oculare e dagli effetti rifrangenti dell’atmosfera. In effetti il seening può facilmente variare durante la stessa serata in maniera imprevedibile. Malgrado tutto sono però riconoscibili una grande quantità di dettagli come piccoli crateri, creste, formazioni montuose e corrugamenti della superficie lavica proprio a ridosso del cratere Burg.
Spostandosi in direzione sud sempre nel settore orientale della Luna, incontriamo il Mare Serenitatis, di forma circolare ed esteso per almeno 650 km. Questa immagine, ripresa a basso ingradimento ponendo la camera CCD al fuoco primario del telescopio, riesce ad inquadrare l’intera vasta struttura del Mare Serenitatis e riesce già a mettere in evidenza alcune sue caratteristiche: all’interno della pianura basaltica che costituisce il Mare, verso il suo bordo più orientale, è possibile osservare due lunghe creste, denominate Dorsa Smirnov e Dorsa Aldrovandi lunghe rispettivamente 131 e 124 km; con una larghezza di pochi km si elevano al di sopra della superficie al massimo per poche centinaia di metri con pendenze non elevate. Si possono meglio osservare quando la luce del Sole le illumina in modo radente, quindi quando si trovano in prossimità del terminatore lunare (la linea che separa il giorno dalla notte sulla Luna). Visibili come “corrugamenti” della superficie dovrebero esseri stati generati dalla solidificazione superficiale della lava fuoriuscita dall’interno lunare diversi miliardi di anni fa a seguito di impatti di asteroidi o di attività interna, che andava a riempire e formare i futuri Mari lunari (Mare Serenitatis in questo caso); mentre la lava che si trovava in superficie si solidifica rapidamente, quella sottostante rimaneva fluida e trascinava gli strati superiori formando queste strutture geologiche. Nella parte nord-orientale del Mare è visibile il grande circolo del cratere Posidonius con diametro di 96 km e parzialmente riempito di lava; in basso verso sud i Montes Haemus con i crateri Menelaus e Plinius posti proprio al confine meridionale del Mare Serenitatis con il Mare Tranquillitatis.
 In questa immagine ripresa con la lente di Barlow 2x rivela alcuni interessanti dettagli sia all’interno del cratere Posidonius ia nelle sue immediate vicinanze. Ricordo che qui la risoluzione si dovrebbe aggirare intorno ai 1,5 km e si notano delle fratture sulla superficie lunare, come delle righe o solchi tracciati nella dura lava basaltica: all’interno del cratere Posidonius stesso, denominato Rima Posidonius e leggermente ad est del cratere ma al di fuori di esso con il nome di Rima G Bond. Si tratta di vere e proprie fratture o faglie nella crosta lunare, e possono essere almeno di tre tipi: di forma sinuosa che rappresentano antichi fiumi di lava o tunnel al cui interno la lava ha continuato a scorrere mentre la parte superiore si raffreddava, una volta terminato il flusso di magma il tubo è rimasto vuoto e la parte superiore è crollata sotto il suo stesso peso formando il solco; a questo tipo potrebbe appartenere la Rima G Bond. Il secondo tipo sono di forma ad arco e si dovrebbero essere formati quando i flussi di lava che hanno formato i mari si raffreddati, contratti e quindi affondati al di sotto della superficie; il terzo tipo sono rettilinei, come la Rima Posidonius, e si tratta di veri e propri “graben” ovvero di spaccature tra due faglie della crosta lunare, quindi appartenenti ad una tipologia completamente differente dalle due precedenti. Possono essersi creati per movimenti tettonici che hanno provocato la separazione tra due faglie oppure a seguito di eventi particolarmente stressanti che hanno coinvolto la crosta lunare in quella zona, come l’impatto di grossi corpi asteroidali.
In questa immagine ripresa con la lente di Barlow 2x rivela alcuni interessanti dettagli sia all’interno del cratere Posidonius ia nelle sue immediate vicinanze. Ricordo che qui la risoluzione si dovrebbe aggirare intorno ai 1,5 km e si notano delle fratture sulla superficie lunare, come delle righe o solchi tracciati nella dura lava basaltica: all’interno del cratere Posidonius stesso, denominato Rima Posidonius e leggermente ad est del cratere ma al di fuori di esso con il nome di Rima G Bond. Si tratta di vere e proprie fratture o faglie nella crosta lunare, e possono essere almeno di tre tipi: di forma sinuosa che rappresentano antichi fiumi di lava o tunnel al cui interno la lava ha continuato a scorrere mentre la parte superiore si raffreddava, una volta terminato il flusso di magma il tubo è rimasto vuoto e la parte superiore è crollata sotto il suo stesso peso formando il solco; a questo tipo potrebbe appartenere la Rima G Bond. Il secondo tipo sono di forma ad arco e si dovrebbero essere formati quando i flussi di lava che hanno formato i mari si raffreddati, contratti e quindi affondati al di sotto della superficie; il terzo tipo sono rettilinei, come la Rima Posidonius, e si tratta di veri e propri “graben” ovvero di spaccature tra due faglie della crosta lunare, quindi appartenenti ad una tipologia completamente differente dalle due precedenti. Possono essersi creati per movimenti tettonici che hanno provocato la separazione tra due faglie oppure a seguito di eventi particolarmente stressanti che hanno coinvolto la crosta lunare in quella zona, come l’impatto di grossi corpi asteroidali.
 I dettagli elencati a proposito dell’immagine precedente sono qui maggiormente visibili, in questa immagine ripresa con la proiezione dell’oculare 9 mm ortoscopico che porta la risoluzione massima a circa 1,3 km o anche meno. La foto soffre putroppo in parte di una certa aberrazione cromatica e di disturbi residui legati alla turbolenza atmosferica ed alle forzature introdotte dall’algoritmo di calcolo per l’elaborazione dell’immagine, tuttavia i graben interni a Posidonius (Rimae Posidonius) sono adesso decisamente più chiari e si può verificare che si tratta di un complesso di fratture e non di una sola. Risulta anche evidente la Rima Chacornac che attraversa l’omonimo cratere a sud di Posidonius che nell’immagine precedente era quasi completamente invisibile e molto più netta la Rima G Bond ad est.
I dettagli elencati a proposito dell’immagine precedente sono qui maggiormente visibili, in questa immagine ripresa con la proiezione dell’oculare 9 mm ortoscopico che porta la risoluzione massima a circa 1,3 km o anche meno. La foto soffre putroppo in parte di una certa aberrazione cromatica e di disturbi residui legati alla turbolenza atmosferica ed alle forzature introdotte dall’algoritmo di calcolo per l’elaborazione dell’immagine, tuttavia i graben interni a Posidonius (Rimae Posidonius) sono adesso decisamente più chiari e si può verificare che si tratta di un complesso di fratture e non di una sola. Risulta anche evidente la Rima Chacornac che attraversa l’omonimo cratere a sud di Posidonius che nell’immagine precedente era quasi completamente invisibile e molto più netta la Rima G Bond ad est.
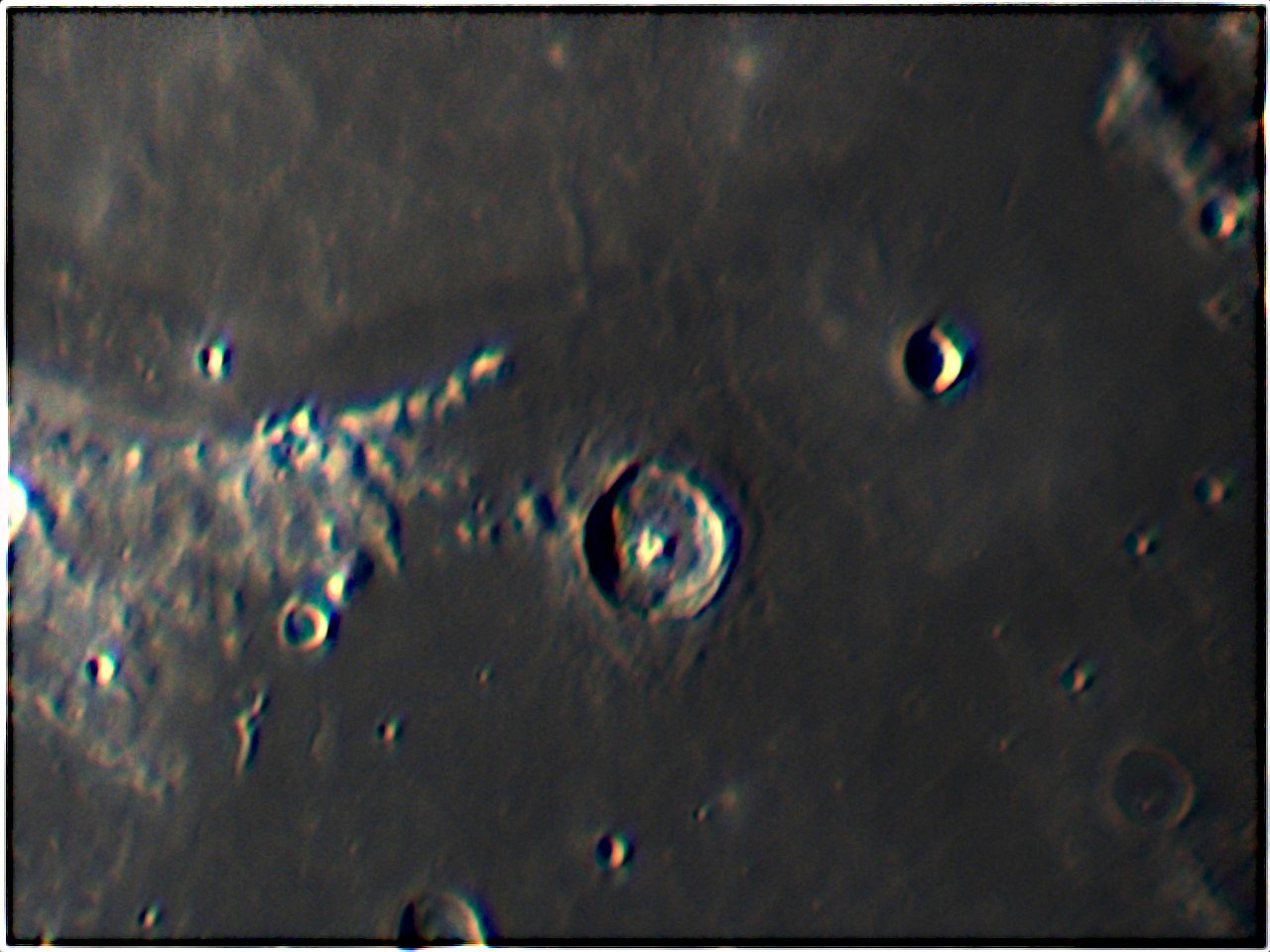 Ancora grazie alla proiezione dell’oculare da 9 mm ortoscopico possiamo ammirare i dettagli del cratere Plinius posto all’estremità meridionale del Mare Serenitatis a ridosso del Mare Tranquillitatis.
Ancora grazie alla proiezione dell’oculare da 9 mm ortoscopico possiamo ammirare i dettagli del cratere Plinius posto all’estremità meridionale del Mare Serenitatis a ridosso del Mare Tranquillitatis.
 L’immagine a bassa risoluzione che comprende gran parte del Mare Traquillitatis ancora più a sud delle foto precedenti, con il cratere Plinius in alto come riferimento.
L’immagine a bassa risoluzione che comprende gran parte del Mare Traquillitatis ancora più a sud delle foto precedenti, con il cratere Plinius in alto come riferimento.
 Procediamo ancora più a sud, dopo il Mare Tranquillitatis incontriamo la strozzatura rappresenta dalla tormentata pianura basaltica della Sinus Asperitatis ed approdiamo infine nel bacino del Mare Nectaris di forma decisamente circolare con una estensione di 350 km. A nord il Mare Nectaris è delimitato dai due grandi crateri Theophilus (101 km di diametro) e Cyrillus (98 km) con Madler (28 km di diametro) che si erge solitario come una sentinella nel punto di passaggio tra il Mare a sud e la Sinus Asperitatis a nord. A sud il Mare Nectaris è delimitato dal grande circo del cratere Fracastorius (124 km di diametro) parzialmente riempito dalla lava che aveva invaso il Mare Nectaris stesso ed annulato la parte nord del bordo del cratere. All’interno del Mare sono già visibili, malgrado l’immagine presentata sia stata ripresa a bassa risoluzione, creste e dorsali che saranno meglio visibili nella foto ripresa con l’oculare da 9 mm ortoscopico presentata nel seguito.
Procediamo ancora più a sud, dopo il Mare Tranquillitatis incontriamo la strozzatura rappresenta dalla tormentata pianura basaltica della Sinus Asperitatis ed approdiamo infine nel bacino del Mare Nectaris di forma decisamente circolare con una estensione di 350 km. A nord il Mare Nectaris è delimitato dai due grandi crateri Theophilus (101 km di diametro) e Cyrillus (98 km) con Madler (28 km di diametro) che si erge solitario come una sentinella nel punto di passaggio tra il Mare a sud e la Sinus Asperitatis a nord. A sud il Mare Nectaris è delimitato dal grande circo del cratere Fracastorius (124 km di diametro) parzialmente riempito dalla lava che aveva invaso il Mare Nectaris stesso ed annulato la parte nord del bordo del cratere. All’interno del Mare sono già visibili, malgrado l’immagine presentata sia stata ripresa a bassa risoluzione, creste e dorsali che saranno meglio visibili nella foto ripresa con l’oculare da 9 mm ortoscopico presentata nel seguito.
 Il sistema dei due crateri appaiati Theophilus e Cyrillus con il solitario Madler immortalati in questa immagine con la Barlow 2x. Il livello del dettaglio è abbastanza soddisfacente e sono visibili una grande quantità di particolari. Ben evidenti sono i picchi centrali multipli di Theophilus e le formazioni di dorsali e creste ai bordi del mare. Ancora una volta ricordo che la risoluzione è qui pari a circa 1,5 km.
Il sistema dei due crateri appaiati Theophilus e Cyrillus con il solitario Madler immortalati in questa immagine con la Barlow 2x. Il livello del dettaglio è abbastanza soddisfacente e sono visibili una grande quantità di particolari. Ben evidenti sono i picchi centrali multipli di Theophilus e le formazioni di dorsali e creste ai bordi del mare. Ancora una volta ricordo che la risoluzione è qui pari a circa 1,5 km.
 Fotografando con l’oculare ortoscopico da 9 mm la parte più orientale del Mare Nectaris e selezionando con cura alcuni parametri della ripresa come il guadagno, il gamma e l’esposizione, vengono messi in risalto una grande quantità di particolari che nella foto a bassa risoluzione erano molto poco o per nulla evidenti: innanzi tutto il cratere Daguerre con i suoi 46 km di diametro che può essere considerato quasi un cratere “fantasma”, quasi completamente colmato di lava; poi il complesso di corrugamenti, creste e dorsali sui bordi orientali del mare, ben visibili con la luce del Sole radente, che sembrano quasi delle colossali onde congelate nel tempo che vanno ad infrangersi sui contrafforti dei Montes Pyrenaeus. Questa catena montuosa si eleva fino a 3000 metri al di sopra della superficie del Mare Nectaris.
Fotografando con l’oculare ortoscopico da 9 mm la parte più orientale del Mare Nectaris e selezionando con cura alcuni parametri della ripresa come il guadagno, il gamma e l’esposizione, vengono messi in risalto una grande quantità di particolari che nella foto a bassa risoluzione erano molto poco o per nulla evidenti: innanzi tutto il cratere Daguerre con i suoi 46 km di diametro che può essere considerato quasi un cratere “fantasma”, quasi completamente colmato di lava; poi il complesso di corrugamenti, creste e dorsali sui bordi orientali del mare, ben visibili con la luce del Sole radente, che sembrano quasi delle colossali onde congelate nel tempo che vanno ad infrangersi sui contrafforti dei Montes Pyrenaeus. Questa catena montuosa si eleva fino a 3000 metri al di sopra della superficie del Mare Nectaris.
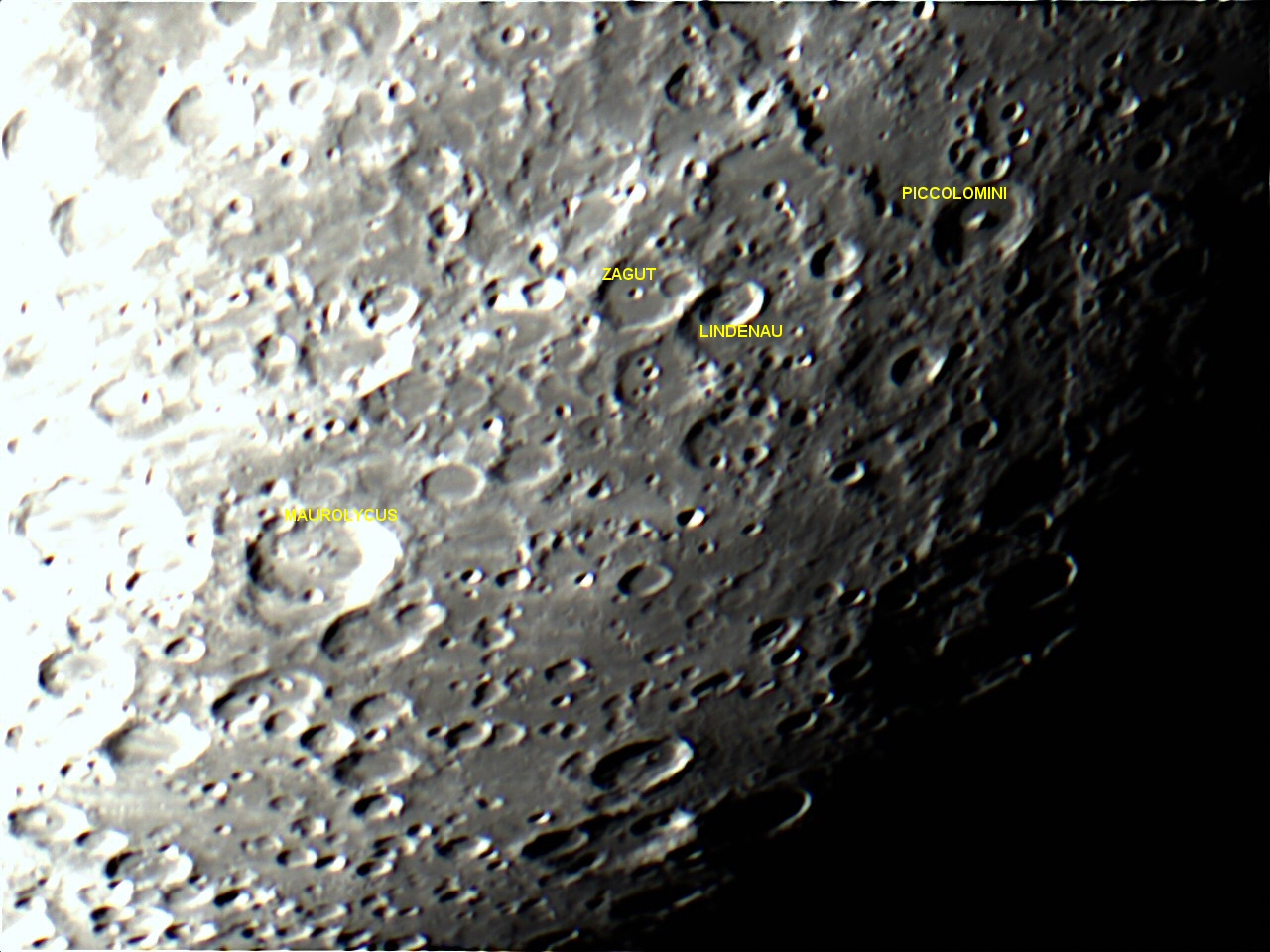 Per concludere questa galleria fotografica interamente realizzata la notte tra il 7 e 8 agosto 2020, un’immagine del tormentato e fortemente craterizzato polo sud lunare, nella sua parte più orientale. Quella presentata qui in alto è una foto a bassa rioluzione, mentre quella seguente è stata realizzata con la lente di Barlow 2x ed è centrata sul cratere Piccolomini, del diametro di 88 km.
Per concludere questa galleria fotografica interamente realizzata la notte tra il 7 e 8 agosto 2020, un’immagine del tormentato e fortemente craterizzato polo sud lunare, nella sua parte più orientale. Quella presentata qui in alto è una foto a bassa rioluzione, mentre quella seguente è stata realizzata con la lente di Barlow 2x ed è centrata sul cratere Piccolomini, del diametro di 88 km.
Conclusioni
Per concludere questa prima parte volevo innanzi tutto ringraziare tutti i lettori per essere arrivati fino a questo punto; spero che gli argomenti trattati siano stati interessanti e siano riusciti a catturare la Vostra attenzione. L’intento è chiaramente quello di illustrare, specialmente ai neofiti, quali possano essere le tecniche e le metodologie per poter osservare e riprendere fotograficamente i corpi celesti, cercando di trarne la massima soddisfazione possibile. Chiunque si cimenti nell’osservazione dei cieli porta dentro di sè quegli spunti di curiosità e senso del meraviglioso che hanno animato gli esseri umani più intelligenti ed intraprendenti della storia. Dal mio punto di vista non basta “fare una bella foto” per essere soddisfatti del proprio lavoro: è necessario capire sia come è possibile arrivare a certi risultati e come si possa sempre migliorare; inoltre la comprensione delle leggi fisiche che stanno dietro i fenomeni che si osservano, il capire “perchè” un qualcosa che vediamo è fatto in un certo modo e non in un altro e quale è la stata la sua storia evolutiva sono per me aspetti fondamentali ed inscindibili dalla ricerca della bellezza nella natura. Le foto presentate non devono essere intese come un’esposizione per vanto ma piuttosto uno spunto per tutti gli altri a voler fare ancora meglio, a capire molto più in profondità i fenomeni e gli scenari che esse rappresentano.
Se sarò riuscito a suscitare curiosità ed interesse anche in sola persona, allora credo che avrò assolto al mio compito.
Massimo Dionisi
Sassari, 18 agosto 2020

